Vol. 6 No. 2 (2022)
Research Articles

The Spinning Electron

PDF
Erratum Editorial History
  • John Lekner
John Lekner
School of Chemical and Physical Sciences, Victoria University of Wellington, Wellington, New Zealand
Bio
DOI: https://doi.org/10.36253/Substantia-1630

Published 2022-09-01

Keywords

  • Electron,
  • Spin,
  • Spinor

How to Cite

Lekner, J. (2022). The Spinning Electron. Substantia, 6(2), 7–13. https://doi.org/10.36253/Substantia-1630

Copyright (c) 2022 John Lekner

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Crossref
Scopus
Google Scholar
Europe PMC

Abstract

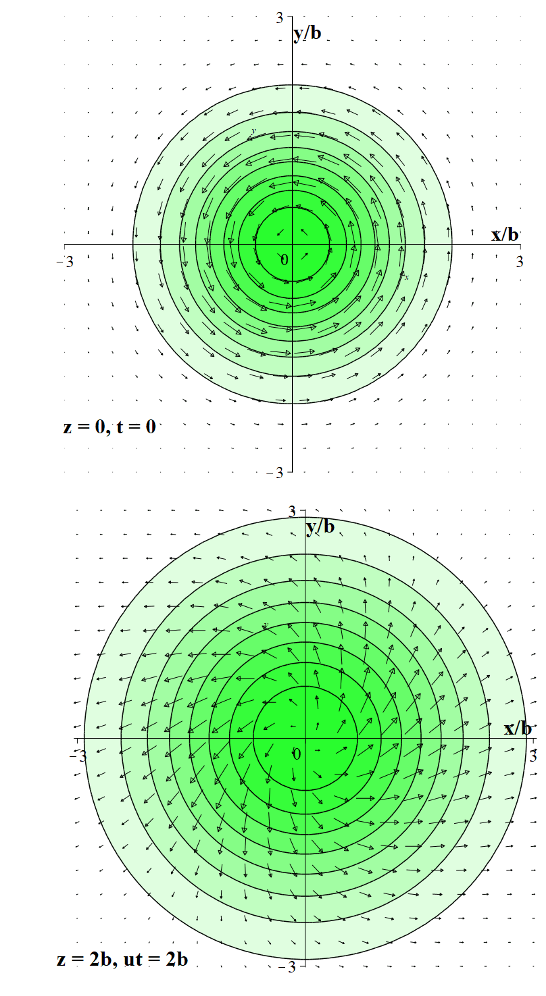
The notion introduced by Ohanian that spin is a wave property is implemented, both in Dirac and in Schrödinger quantum mechanics. We find that half-integer spin is the consequence of azimuthal dependence in two of the four spinor components, relativistically and non-relativistically. In both cases the spinor components are free particle wavepackets; the total wavefunction is an eigenstate of the total angular momentum in the direction of net particle motion. In the non-relativistic case we make use of the Lévy-Leblond result that four coupled non-relativistic wave equations, equivalent to the Pauli-Schrödinger equation, represent particles of half-integer spin, with g-factor 2. An example of an exact Gaussian solution of the non-relativistic equations is illustrated.

PDF
Erratum Editorial History

References

  1. Ohanian H C “What is spin?”, Am. J. Phys. 54, 500-505 (1986).
  2. Belinfante F J “On the spin angular momentum of mesons”, Physica 6, 887-898 (1939).
  3. Dirac P A M “The quantum theory of the electron”, Proc. Roy. Soc. A 117, 610-624 (1928).
  4. Dirac P A M “The quantum theory of the electron. Part II”, Proc. Roy. Soc. A 118, 351-361 (1928).
  5. Griffiths D J, Introduction to quantum mechanics, 2ed (Prentice Hall, New Jersey, 2005), Section 4.4.
  6. Lévy-Leblond J-M “Nonrelativistic particles and wave equations”, Commun. Math. Phys. 6, 286-311 (1967).
  7. Galindo A and del Rio C S “Intrinsic magnetic moment as a nonrelativistic phenomenon”, Am. J. Phys. 29, 582-584 (1961).
  8. Lekner J, Theory of electromagnetic pulses (Institute of Physics Publishing 2018), Section 2.6.
  9. Bliokh K Y, Dennis M R and Nori F “Relativistic electron vortex beams: angular momentum and spin-orbit interaction”, Phys. Rev. Lett. 107, 174802 (2011).
  10. Greiner W, Quantum mechanics, 3ed (Springer, Berlin, 1994), Chapter 13.
  11. Kennard E H “Zur Quantenmechanik einfacher Bewegungstypen”, Z. Physik 44 326-352 (1927).
  12. Darwin C G “Free motion in wave mechanics”, Proc. Roy. Soc. Lond. A117, 258-293 (1927).
  13. Lekner J “Rotating wavepackets”, Eur. J. Phys. 29, 1121-1125 (2008).
  14. Gould R J “The intrinsic magnetic moment of elementary particles”, Am. J. Phys. 64, 597-601 (1996).
  15. Lévy-Leblond J-M “The total probability current and the quantum period”, Am. J. Phys. 55, 146-149 (1987).
  16. Mita K “Virtual probability current associated with the spin”, Am. J. Phys. 68, 259-264 (2000).
  17. Landau L D and Lifshitz E M, Quantum mechanics, 2ed. (Pergamon, Oxford, 1985).